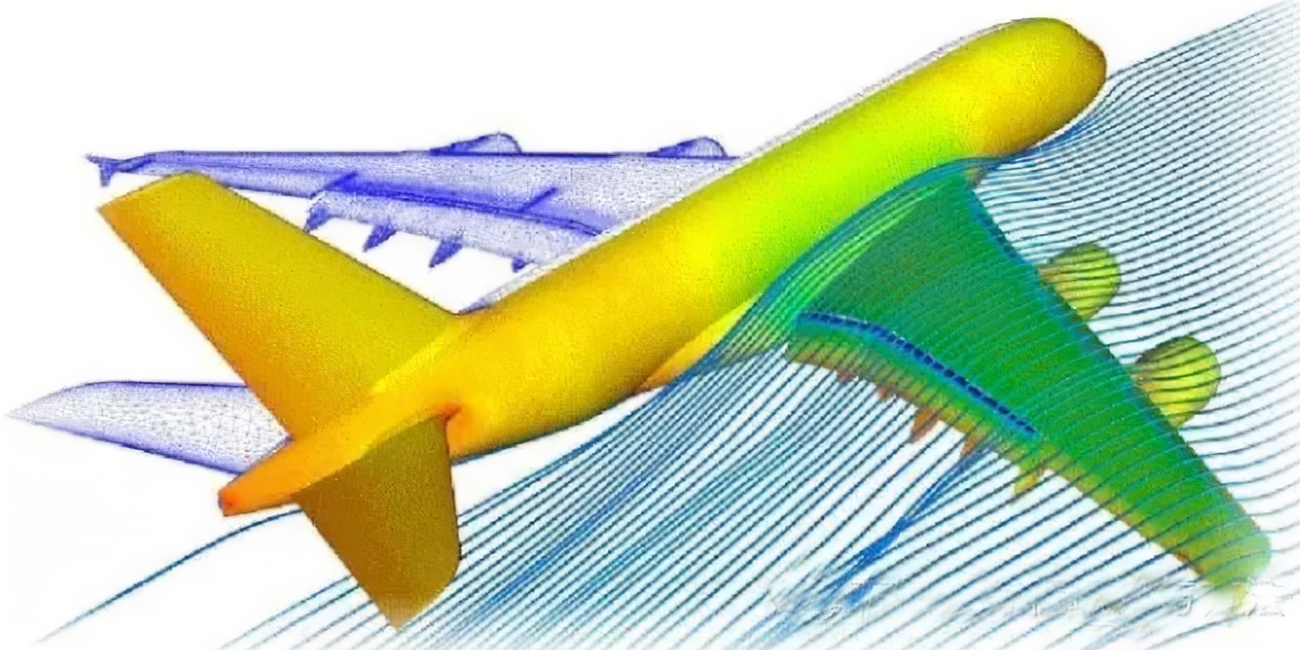
在当今科学与工程领域,有一项神秘而强大的技术正在默默地支撑着无数项目的实现与发展。这项技术就是“有限元分析”。虽然对大多数人来说,这个名词可能有些陌生,但它却是现代科技进步的重要驱动力。让我们一起探索这个神秘而令人着迷的领域,揭开有限元分析的神秘面纱。
有限元分析是一种数值模拟方法,用于解决复杂工程和科学问题。它的原理源自上世纪50年代早期,当时工程师们在解决结构力学问题时遇到了巨大困境。传统解析方法往往无法应对复杂几何形状、非线性行为和材料异质性等问题,这促使科学家寻求一种全新的方法。
有限元分析的核心思想是将复杂的实体分割成许多简单的、称为“有限元”的小块。这些有限元可以是三角形、四边形、六边形或其他形状,取决于问题的性质。通过在每个有限元内建立数学模型,并运用适当的数学算法,工程师和科学家可以模拟出整个结构或系统的行为。这种方法的优势在于它可以近似地描述复杂问题,同时又保持较高的计算效率。
有限元分析在各个领域都有广泛的应用。例如,在航空航天工程中,它被用于优化飞机的机翼设计,以提高飞行性能并降低燃油消耗。在汽车工业中,有限元分析可以模拟车辆在碰撞时的受力情况,从而改善车辆的安全性能。在建筑工程中,它可以帮助设计师评估建筑物的结构强度,确保其在自然灾害面前的抗击能力。
然而,尽管有限元分析在科学与工程领域展现出巨大的潜力,但它仍然面临着一些挑战。其中之一是模型精度的问题。在建立数学模型时,必须对问题进行适当的简化和假设,以降低计算复杂度。但这可能导致模拟结果与实际情况之间存在一定的偏差。因此,工程师和科学家需要不断优化模型,以获得更加准确的结果。
此外,有限元分析的应用还需要高度专业的技能和经验。对于复杂的工程系统,模型的建立和分析需要深厚的理论知识和实践经验。因此,培养优秀的有限元分析工程师成为了当今科技教育的重要任务。
总体而言,有限元分析是一门令人着迷且不断演进的科学与工程领域。它为我们理解和解决复杂问题提供了强大的工具,推动着科技的不断进步。随着计算机技术的不断发展和算法的改进,我们有理由相信有限元分析的应用将越来越广泛,带来更多前所未有的创新与突破。让我们迎接这个未知之域,探索其中的无尽奇妙!