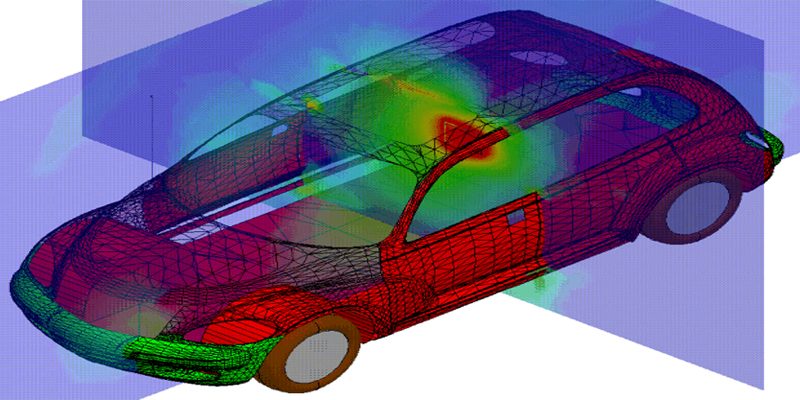
在科学与工程领域,有一项技术已经引起了广泛的兴趣和追捧,它就是“有限元分析”。或许在日常生活中,我们难以感知这个看似复杂的名词背后蕴含的深远影响,然而,正是有限元分析在材料、结构和流体力学等领域中的革命性角色,塑造并改变了我们的世界。
有限元分析的核心思想十分简洁,却蕴含着无限的可能性。它通过将复杂的结构、系统或物体划分为许多小的几何单元,如三角形或四边形,在每个单元内求解微分方程,然后将这些单元按照一定规则组合起来,得到整体系统的行为特性。这种方法的精妙之处在于,它将复杂的问题简化为许多小的、容易处理的部分,从而大大降低了计算的难度。
正是有限元分析的这种独特方法,使得科学家和工程师们能够更深入地研究各种问题。以材料科学为例,研究人员可以利用有限元分析来模拟不同材料在不同环境下的性能表现,预测其在受力时的变形和破坏情况。这种能力不仅可以为新材料的开发提供指导,还可以在设计阶段发现潜在的问题,从而节省时间和成本。
在工程领域,有限元分析更是如鱼得水。无论是建筑物的结构设计、飞机的气动性能研究,还是汽车的碰撞安全性分析,都离不开有限元分析的应用。通过模拟真实工况下的受力情况,工程师们可以更好地了解系统的强度、刚度和稳定性,从而进行精准的优化。这项技术的应用不仅加速了新产品的推出,也提升了现有产品的质量和可靠性。
然而,有限元分析也并非完美无缺。尽管它在简化复杂问题方面表现出色,但模型的准确性仍然依赖于对物理现象的准确建模和参数的合理选择。不当的假设或误差可能导致结果的失真,因此在使用有限元分析时,科学家和工程师们仍需要保持谨慎和批判性思维。
总之,有限元分析作为一项革命性的技术,已经在科学与工程领域产生了深远的影响。它的应用不仅拓展了我们对材料和结构行为的理解,也加速了创新的步伐。随着计算能力的不断提升和方法的不断改进,有限元分析必将继续引领着科学与工程的发展,为我们揭示出更多未见底的奥秘。