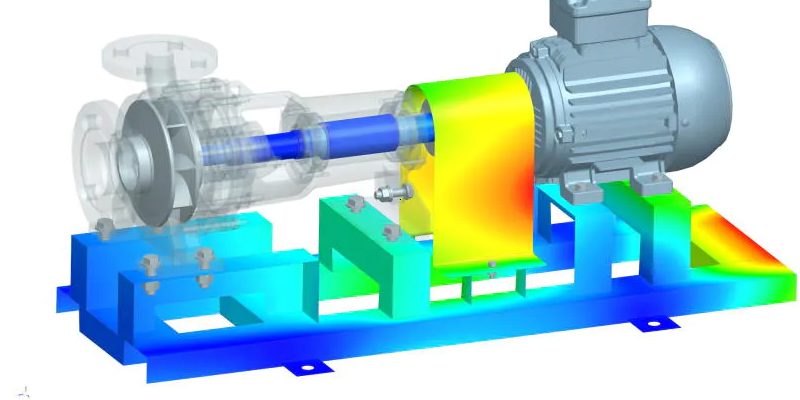
有限元分析(Finite Element Analysis,简称FEA)是工程领域中一项强大的数字工具,它在设计和分析各种结构和系统方面发挥着至关重要的作用。本文将深入探讨有限元分析的原理、应用领域以及其在工程设计中的重要性。
有限元分析的原理
有限元分析的核心原理是将复杂的结构或系统分割成许多小的有限元,然后分别对每个有限元进行数值计算,最后将它们组合在一起以获得整体系统的行为。这种分析方法可以模拟各种力、应变和热传导等物理现象,使工程师能够更好地了解结构的性能。
具体来说,有限元分析涉及以下步骤:
1. 几何建模:首先,需要将要分析的结构或系统进行几何建模,将其划分为有限元。这通常涉及使用CAD(计算机辅助设计)软件来创建几何模型。
2. 网格生成:接下来,将模型划分为小的有限元,并生成一个网格,每个有限元都可以在其内进行数值计算。这个过程通常由有限元分析软件自动完成。
3. 边界条件和加载:在进行分析之前,必须定义结构的边界条件(如支座或固定边界)以及加载条件(如受力或热源)。这些条件对于准确模拟结构行为至关重要。
4. 数值计算:一旦设置好模型和边界条件,就可以进行数值计算,求解每个有限元中的物理方程。这通常涉及解线性代数方程组,其中包含了各种力学和热力学方程。
5. 结果后处理:最后,需要对计算结果进行后处理,以获得有关应力、应变、温度分布等参数的信息。这些结果可以用于评估结构的性能和安全性。
应用领域
有限元分析在各种工程领域中都有广泛的应用,包括但不限于以下几个方面:
1. 结构工程:在建筑、桥梁、飞机、汽车等领域中,有限元分析可用于评估结构的强度、刚度和稳定性,以确保其满足设计要求。
2. 热力学和流体力学:有限元分析可以用于模拟热传导、流体流动和传热问题,例如热交换器和管道系统的设计。
3. 电子和电气工程:在电路板、电机和传感器的设计中,有限元分析可用于预测电磁场分布、热耦合和结构稳定性。
4. 医疗器械:有限元分析可以用于模拟植入式医疗器械在人体内的行为,以确保其安全性和性能。
工程设计中的重要性
有限元分析在工程设计中的重要性不言而喻。它可以帮助工程师:
1. 优化设计:通过在数字模型中进行多次分析,工程师可以优化结构的设计,减少材料使用、提高性能并降低成本。
2. 评估安全性:有限元分析可以帮助工程师评估结构的安全性,确保其在受到外部载荷或温度变化时不会发生失效或损坏。
3. 节省时间和资源:与传统的试验和试错方法相比,有限元分析可以节省大量的时间和资源,因为它允许在计算机上模拟各种情况。
4. 支持决策:基于有限元分析的结果,工程师可以更好地支持设计决策,并为客户和利益相关者提供可靠的数据。
总的来说,有限元分析是现代工程设计不可或缺的一部分,它为工程师提供了一种强大的工具,可以更好地理解和优化复杂系统的行为,从而推动技术的不断进步。在今天的数字时代,它已成为工程领域的一项数字神奇。