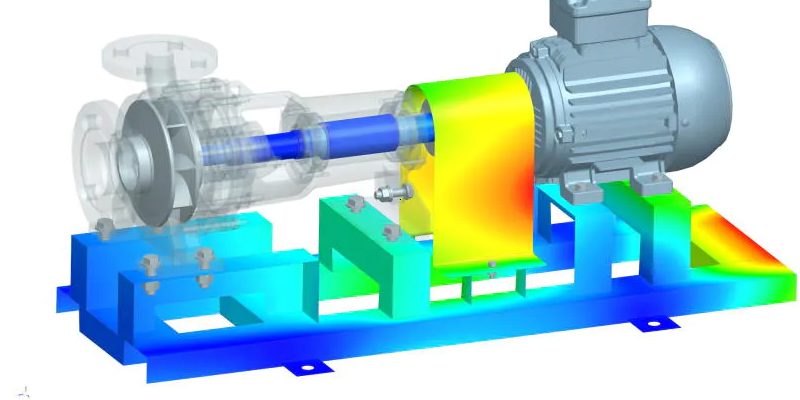
有限元分析(Finite Element Analysis,简称FEA)是一种数值模拟方法,用于解决工程和科学领域中的各种复杂问题。它的应用范围广泛,涵盖了结构力学、热传导、流体力学、电磁场等多个领域。FEA的核心思想是将复杂的实体分割成小的有限元,然后通过求解这些元素的行为来近似模拟整个系统的行为。本文将探讨有限元分析的原理、应用以及它对未来工程领域的潜在影响。
有限元分析的基本原理
有限元分析的核心思想是将连续体分解成许多小的子区域,即有限元,然后在每个有限元内解决力学或物理方程,最后将这些子区域的解耦合以获得整个系统的解。这一过程通常包括以下几个步骤:
1. 建模: 首先,需要将要分析的系统建模成有限元模型。这涉及到将物体分割成有限元,确定边界条件和加载条件。
2. 离散化: 每个有限元内部的物理行为可以由一组方程来描述,例如弹性力学中的应力-应变关系。这些方程通常是偏微分方程,需要进行数值离散化,将连续问题转化为离散问题。
3. 求解: 通过求解离散方程组,可以获得每个有限元的位移、应力、温度等信息。
4. 后处理: 最后,需要将每个有限元的结果耦合在一起,以获得整个系统的行为。这通常包括绘制应力分布、温度分布、位移分布等。
应用领域
有限元分析在工程领域的应用非常广泛,以下是一些典型的应用领域:
1. 结构分析: 有限元分析可用于评估建筑物、桥梁、飞机和汽车等结构的强度和刚度,以确保它们在各种负载下的安全性和性能。
2. 热传导分析: FEA可用于模拟热传导问题,如热沉降、散热器设计和电子设备的温度分布。
3. 流体力学: 在流体力学中,有限元分析可用于模拟液体和气体流动,如风洞测试和水力学分析。
4. 电磁场分析: FEA还可用于分析电磁场问题,如电磁屏蔽、电机设计和电磁场传感器。
5. 医学应用: 在医学领域,有限元分析可以用于模拟骨骼力学、生物材料性能以及医疗设备的设计。
未来的潜在影响
有限元分析的应用领域不断扩展,并且在工程领域的革命性影响正在逐渐显现。以下是一些潜在的影响:
1. 智能化设计: 随着计算能力的不断提高,工程师将能够使用FEA进行更复杂的设计和优化。机器学习和人工智能技术的融合将使智能化设计成为可能,从而大幅缩短产品开发周期。
2. 材料创新: 有限元分析有助于更深入地理解材料的行为,这将推动材料科学的发展。新材料的设计和合成将更具精确性,以满足不同应用的需求。
3. 可持续性: FEA可用于模拟可持续性解决方案,如风能和太阳能设备的设计,以及减少废物和能源消耗的新型工程技术。
4. 虚拟原型: FEA的广泛应用将减少实际原型的制造需求,从而减少资源浪费。工程师可以在虚拟环境中测试各种设计,以找到最佳解决方案。
总之,有限元分析是一个强大的工程工具,已经在多个领域产生了深远的影响。随着技术的不断进步,它将继续推动工程领域的革命,为我们创造更安全、更高效、更可持续的世界。