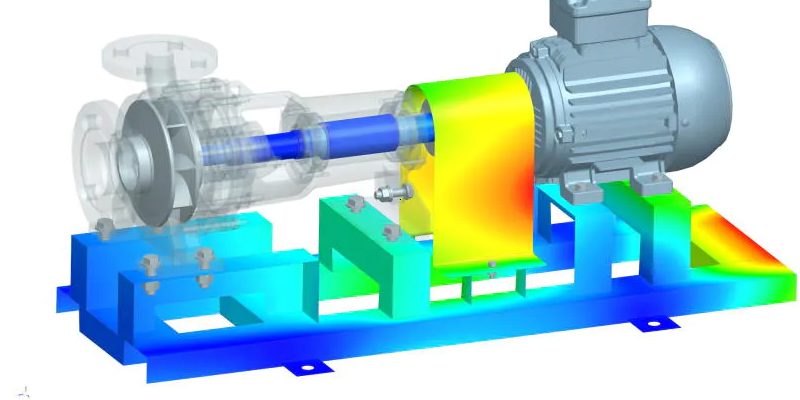
有限元分析(Finite Element Analysis,简称FEA)是一种在工程领域中革命性的数值模拟技术,已经在设计、优化和测试各种结构和系统方面取得了巨大的成功。FEA的原理基于将复杂的现实结构分解为无数小的有限元,然后通过数学方法来模拟它们的行为。这一技术的广泛应用使得我们能够在实际制造之前对产品进行全面的性能评估,从而节省时间和成本。
有限元分析最初在航空航天领域得到了广泛应用,用于设计和分析飞机和宇宙飞船的结构。然而,随着计算机技术的不断发展,FEA的应用领域迅速扩展到了汽车制造、建筑工程、医疗设备、电子产品等各个领域。以下是有限元分析在不同领域的独特应用:
汽车工业:在汽车设计中,FEA可用于优化车身结构,提高碰撞安全性和降低燃油消耗。它还能模拟引擎零件的热应力和振动特性,以改进引擎性能。
建筑工程:建筑师和工程师可以使用FEA来评估建筑物的抗地震性能,预测结构的变形,确保建筑物的安全性和耐久性。
医疗设备:医疗设备制造商可以使用FEA来模拟医疗设备的机械性能,如人工关节或心脏起搏器。这有助于改进设计,减少手术风险。
电子产品:在电子产品设计中,FEA可用于分析电路板的热特性,以确保设备在长时间使用时不会过热。
石油和天然气:在石油和天然气行业,FEA可用于评估管道和油井的强度,以应对极端的地下环境条件。
化工工程:化学工程师可以使用FEA来模拟反应器和管道的化学过程,以改进生产效率和安全性。
FEA的独特之处在于它提供了在物理实验之前进行虚拟测试和优化的能力。这不仅加速了产品开发周期,还减少了制造和测试成本。此外,FEA还有助于减少对资源的浪费,使产品更环保。
虽然有限元分析已经在工程领域取得了巨大的成功,但它仍在不断发展和改进中。随着计算机性能的提升和仿真软件的不断完善,FEA将继续发挥其独特的作用,推动工程领域的创新和进步。无限可能性正等待着工程师和设计师,他们可以通过FEA来实现更安全、更高效、更创新的产品和结构。