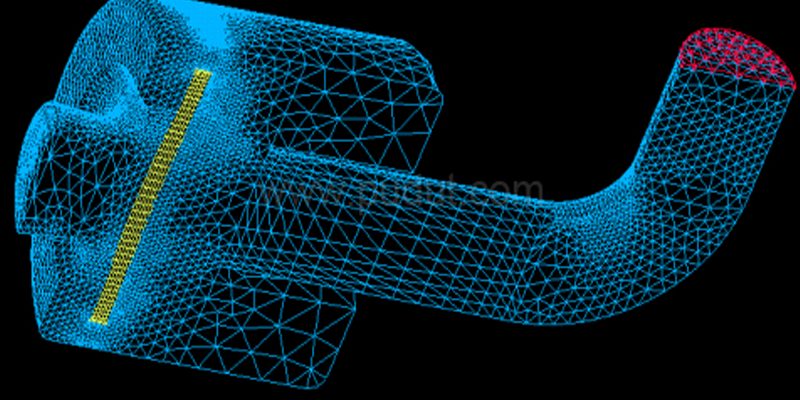
在利用Abaqus进行薄壳结构(如航空航天蒙皮、船舶壳体、储罐等)的稳定性分析时,局部失稳(Local Buckling)是常见的失效模式。其特征表现为结构在压应力作用下,在局部区域发生突然的、小范围的屈曲变形。精确预测此类现象极具挑战性,而网格划分的质量往往是决定分析成败与精度高低的关键因素。不恰当的网格会导致计算结果严重偏离实际情况,要么无法捕捉失稳模态,要么得到过于刚硬或过于柔软的错误结果。本文将深入探讨网格划分的影响,并提出一套系统的优化方案。
一、 网格划分为何对薄壳失稳分析至关重要?
薄壳局部失稳的本质是结构在高阶模态下失去稳定性。其屈曲波形通常波长较短、形态复杂。有限元法的基本原理是用大量简单单元的集合体来近似复杂的连续体,因此网格必须足够精细才能“分辨”出这些复杂的屈曲形态。
-
捕捉屈曲模态: 粗糙的网格无法描述曲率的连续变化,无法形成光滑的屈曲波形。如果网格尺寸大于局部失稳的半波长,分析将完全无法捕捉到该失稳模式,导致预测的失稳载荷虚高,造成灾难性的设计错误。
-
计算精度: 壳单元(如S4R)的力学响应(应力和应变)基于单元内部的假设位移场计算。粗糙网格会高估单元的抗弯刚度,导致结构显得“过于刚硬”,从而计算出偏高的临界失稳载荷。
-
收敛性: 在后屈曲分析中,粗糙或不合理的网格容易导致严重的网格扭曲,造成求解收敛困难,计算中止。
二、 常见网格问题及其对局部失稳的影响
| 问题 | 表现及影响 | 图示示意 |
|---|---|---|
| 网格过于粗糙 | 无法捕捉细微的屈曲波形,预测的失稳载荷偏高,模态形状不光滑、呈“锯齿状”。 | [粗糙网格产生锯齿状屈曲形态] |
| 网格种子分布不合理 | 在应力梯度大或可能发生屈曲的关键区域网格稀疏,导致无法准确求解该区域响应;非关键区域网格过密,浪费计算资源。 | |
| 单元形状差(畸形度高) | 如过度扭曲的四边形、三角形单元,会引入数值误差,影响计算精度和收敛性,尤其在后屈曲路径分析中问题显著。 | [高扭曲度单元示意图] |
| 网格类型选择不当 | 在主要受力区域大量使用三角形单元(如S3)。虽然三角形单元能适应复杂几何,但其为常应变单元, bending behavior 的精度通常低于四边形单元,可能导致整体刚度偏硬。 |
三、 针对薄壳局部失稳的网格划分优化方案
为解决上述问题,实现高精度、高效率的失稳分析,可采用以下系统化的优化方案:
1. 单元类型优选:首选减缩积分四边形壳单元
-
推荐单元: S4R (4节点减缩积分有限膜应变壳单元) 是大多数薄壳稳定性分析的首选。
-
优点: 减缩积分技术可缓解网格锁死问题,对网格扭曲的容忍度较高,计算效率高,且能很好地模拟屈曲行为。
-
-
慎用单元: 完全积分单元(如S4)在弯曲变形中容易发生剪切锁死,导致过度刚硬,不建议用于失稳分析。三角形单元S3/S3R应仅用于几何过渡区域,且比例应尽可能小。
2. 实施基于屈曲波长的网格敏感性分析
这是确定临界网格尺寸最科学的方法。
-
步骤一: 进行初步的线性特征值屈曲分析(Linear Buckling Analysis)。
-
步骤二: 观察前几阶屈曲模态(特别是最低阶模态),估算屈曲方向的半波长(λ/2)。
-
步骤三: 在屈曲区域,确保网格尺寸小于估算半波长的1/2到1/4(即至少在一个波长内有4-8个单元)。这是捕捉屈曲形态的黄金法则。
-
步骤四: 采用不同网格尺寸(如:10mm, 8mm, 5mm)进行多次非线性分析,观察临界载荷的变化。当继续加密网格,计算结果(如临界载荷)的变化在可接受误差范围内(如<2%)时,即可认为网格已收敛。
3. 智能布种与分区划分
-
关键区域加密: 在高应力区、几何不连续处(如开孔、加强筋连接处)、载荷或边界条件施加处,以及根据初步屈曲分析预测的失稳区域,进行局部网格加密。
-
非关键区域粗化: 在应力变化平缓、远离失稳区域的部位,可以适当放宽网格尺寸,以节省计算成本。
-
使用分区(Partition)工具: 通过分割几何体,可以对不同区域独立布种和控制网格,实现从密到疏的平滑过渡,避免网格突变。
4. 严格控制单元质量
在Mesh模块中使用Mesh Quality Checks检查单元质量。重点关注:
-
翘曲度(Warping): 对于四边形壳单元,应控制在一定范围内。
-
长宽比(Aspect Ratio): 尽量接近1,一般建议小于5:1。
-
内角(Angle): 尽量接近90度,避免出现尖角或钝角。
高质量的网格不仅能提高精度,更能极大改善非线性分析的收敛性。
5. 后屈曲分析的特殊考虑
对于需要分析后屈曲路径(Post-buckling Path)的问题,网格需要更高的鲁棒性。
-
进一步加密: 后屈曲过程中可能伴随复杂的模态跃迁和变形,网格可能需要比仅做屈曲分析时更密一些。
-
使用静力通用分析步: 结合
NLgeom=ON(几何非线性),并采用弧长法(Riks) 来跟踪复杂的荷载-位移路径。此时,高质量的网格是弧长法成功收敛的基础。
四、 最佳实践总结与工作流建议
-
几何清理: 开始前简化不必要的细节(如微小倒角),修复几何缺陷。
-
初步分析: 用较粗的网格进行线性屈曲分析,识别潜在失稳区域和模态。
-
智能布种: 基于初步分析结果,在关键区域设置密集种子,其他区域设置稀疏种子。
-
划分网格: 首选S4R单元,采用结构化(Structured)或扫掠(Swept) 划分技术(如果几何允许),以获得规整的网格。否则使用自由(Free) 划分并严格控制质量。
-
敏感性分析: 执行网格收敛性研究,确保结果对网格尺寸不敏感。
-
提交计算与验证: 运行完整的非线性屈曲分析,并检查结果(变形、应力、载荷-位移曲线)的合理性和收敛性。
结论
在Abaqus中,薄壳结构的局部失稳分析绝非简单地点击“生成网格”即可完成。它是一个需要工程师深刻理解物理问题、有限元理论并进行精细操作的过程。将网格视为计算模型的一部分,而非前处理的附属品。通过采用基于屈曲波长的网格敏感性分析、关键区域局部加密、优选单元类型和控制单元质量这一套系统化的优化方案,可以显著提升局部失稳预测的准确性和可靠性,为高性能薄壳结构的设计提供坚实的数据支撑。