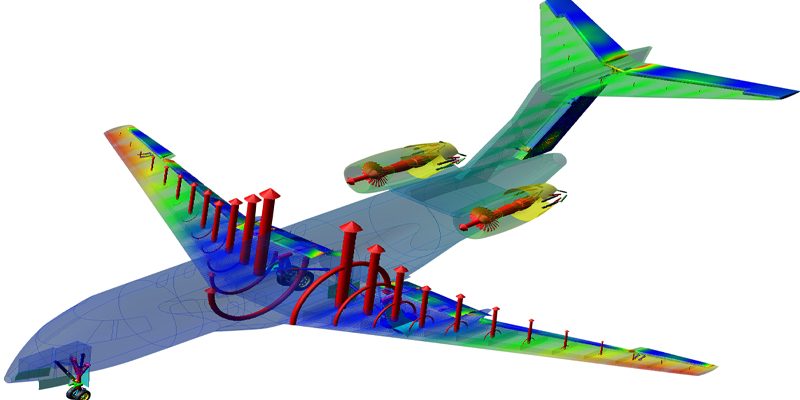
多体动力学分析是一门研究自然界复杂系统行为的关键科学领域。它涉及了研究由多个相互作用的物体组成的系统,这些物体可以是分子、行星、星系或其他形式的粒子集合。通过深入了解多体动力学,我们可以揭示自然界中各种规模的系统之间的共性和差异,这对于科学和工程领域都具有巨大的价值。
多体动力学的基本原理
多体动力学的核心思想是研究系统中各个物体的运动和相互作用。这些物体之间的相互作用可以通过各种力来描述,如引力、电磁力、弹性力等。多体动力学的目标是根据这些相互作用的规律,预测系统的未来行为或回顾系统的过去演化。
在多体动力学中,牛顿的运动定律是一个基本的框架。根据牛顿的第二定律,一个物体的运动状态受到施加在它上面的力的影响。这个定律可以用微分方程的形式表示,通常称为牛顿的运动方程。对于一个多体系统,就会有多个运动方程,每个方程描述一个物体的运动。这些方程一起构成了多体系统的动力学模型。
多体动力学的应用领域
多体动力学的应用领域非常广泛,从微观到宏观,涉及到各种自然和工程系统。以下是一些多体动力学的应用示例:
1. 分子动力学:在化学和生物学中,多体动力学用于模拟和分析分子的运动和相互作用。这对于药物设计、生物分子结构研究和材料科学都是至关重要的。
2. 天体力学:研究星系、行星、卫星等天体之间的运动和相互作用。多体动力学的应用有助于理解太阳系的形成和演化,以及行星的轨道稳定性。
3. 机械系统:在工程领域,多体动力学用于设计和优化机械系统,如汽车悬挂系统、飞机起落架和机械臂。
4. 社会网络分析:在社会科学中,多体动力学可以用来研究社会网络中个体的行为和相互关系,从而揭示社会结构和信息传播的模式。
多体动力学的挑战和未来展望
尽管多体动力学在各个领域都有广泛的应用,但它也面临着一些挑战。其中之一是系统规模的增加,导致方程组的复杂性急剧增加。为了解决这个问题,研究人员正在不断发展高性能计算方法和数值模拟技术,以处理大规模多体系统的动力学问题。
此外,多体动力学还需要处理不确定性和噪声。在许多实际应用中,系统参数可能不是完全已知的,同时外部扰动和噪声也会影响系统的行为。因此,研究人员需要开发具有鲁棒性的方法,以应对这些不确定性。
未来,随着技术的不断进步,多体动力学将继续在科学和工程领域发挥关键作用。它将有助于我们更深入地理解自然界的复杂系统,从而推动科学和技术的进步,解决一些关键的挑战,如气候变化、医学疾病和能源可持续性等问题。多体动力学将继续为我们揭示自然界奥秘提供重要的工具和洞察力。