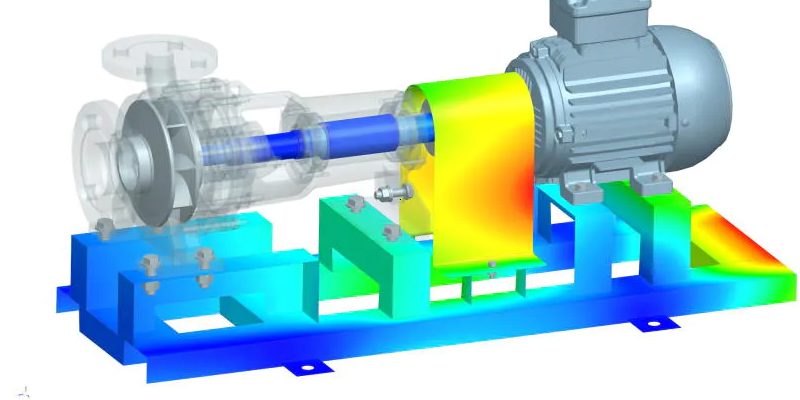
有限元分析(Finite Element Analysis,简称FEA)是一种工程分析方法,旨在模拟和评估物体在不同条件下的力学行为。它已经成为工程界不可或缺的工具,可以用于解决各种工程和科学问题。本文将介绍有限元分析的基本原理、应用领域以及其在现代工程中的重要性。
1. 有限元分析的基本原理
有限元分析的核心思想是将复杂的物体分解成许多小的有限元素,然后通过求解这些元素的行为来近似整个物体的行为。这些元素可以是线性的或非线性的,可以代表各种材料的性质。有限元分析的基本步骤包括:
1.1. 几何建模
首先,需要将要分析的物体建模为一个有限元网格。这个网格通常包含许多节点和元素,节点定义了物体的几何形状,元素用于近似物体的行为。这一步骤要求对物体的几何形状有深入的了解。
1.2. 材料属性
每个元素都需要被赋予材料属性,如弹性模量、泊松比等。这些属性描述了材料如何响应力和变形。不同的材料具有不同的性质,因此这一步骤至关重要。
1.3. 边界条件
在分析中,需要指定边界条件,包括约束和加载。约束定义了哪些部分的物体是固定的,加载则模拟了外部施加的力或压力。这些条件对于分析结果具有重大影响。
1.4. 求解方程
一旦建立了有限元模型并定义了边界条件,就可以使用数值方法来求解力学方程。通常,这涉及到解线性或非线性代数方程组,以确定每个节点的位移和应力。
1.5. 后处理
最后,需要对分析结果进行后处理,以获取有关位移、应力、应变等信息。这些结果可以用于评估物体的性能,并进行必要的设计改进。
2. 应用领域
有限元分析在各种工程和科学领域中都有广泛的应用,包括但不限于:
2.1. 结构工程
在结构工程中,有限元分析用于评估建筑物、桥梁、飞机、汽车等的强度和稳定性。工程师可以使用FEA来优化设计,以确保结构在各种条件下都能安全运行。
2.2. 汽车工业
汽车制造商使用有限元分析来模拟碰撞测试、振动和噪音分析,以改进汽车的安全性和性能。
2.3. 航空航天
在航空航天工业中,有限元分析用于设计飞机、卫星和火箭的结构,并评估其在大气层内外的性能。
2.4. 医疗领域
医疗设备的设计和生物力学研究也受益于有限元分析。它可以用于模拟人体组织的行为,以改进医疗设备和手术过程。
2.5. 石油和天然气
在石油和天然气行业,有限元分析用于评估管道、油井和设备的耐久性和安全性,以减少事故风险。
3. 现代工程中的重要性
有限元分析的重要性在现代工程中不断增加。它允许工程师更好地理解复杂系统的行为,降低设计风险,提高产品性能,并减少开发周期。此外,随着计算能力的提高,有限元分析变得更加精确和高效。
总之,有限元分析是一种强大的工程工具,它通过将复杂的问题简化为小的可管理部分,使工程师能够更好地理解和优化各种系统。在不断发展的技术和工程领域,有限元分析将继续发挥关键作用,帮助解决未来的工程挑战。