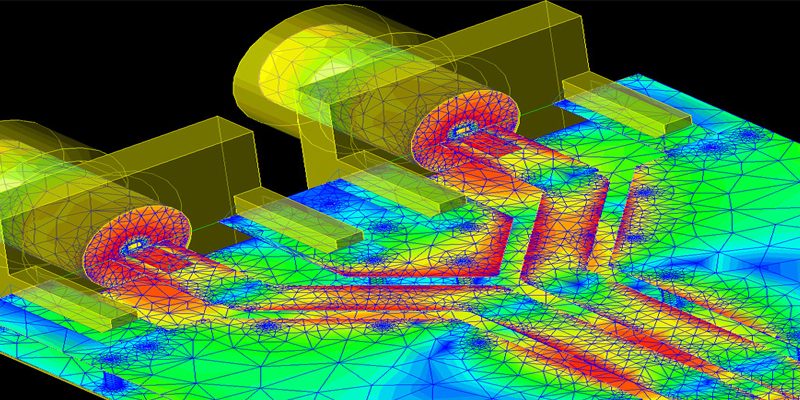
有限元分析是一种在工程领域广泛应用的数值模拟方法,它在设计、优化和分析各种结构和系统中发挥着关键作用。本文将介绍有限元分析的一些新的前沿应用和挑战,展示这一领域的最新发展和创新。
引言
有限元分析(Finite Element Analysis,FEA)已经成为现代工程领域不可或缺的工具之一。它通过将复杂的结构或系统分解为有限数量的元素,然后应用数学方法来模拟其行为,使工程师和设计师能够更好地理解和优化系统性能。然而,随着技术的不断进步和工程需求的日益增加,有限元分析也不断发展和演进。
新的前沿应用
1. 多物理耦合
传统的有限元分析主要关注结构力学,但现代工程越来越需要考虑多个物理现象的耦合。例如,汽车制造商需要同时考虑结构强度、热传导和流体动力学,以优化车辆性能。多物理有限元分析已经崭露头角,使工程师能够更全面地评估系统的行为。
2. 拓扑优化
拓扑优化是一种基于有限元分析的创新方法,旨在实现最佳结构设计。它通过自动调整材料的分布来减小结构的重量,同时满足性能要求。这一技术在航空航天和汽车工业等领域具有潜在的巨大影响。
3. 材料建模
新材料的开发对工程领域至关重要。有限元分析在材料建模方面也取得了进展,允许工程师更好地模拟新材料的性能,以便更好地应用于实际设计中。
挑战
虽然有限元分析的应用范围不断扩大,但也伴随着一些挑战:
1. 计算资源需求
多物理耦合分析和拓扑优化通常需要大量的计算资源,包括高性能计算机和先进的软件。这对于一些小型企业和研究机构可能是一项挑战。
2. 数据可靠性
有限元分析的结果通常依赖于输入数据的准确性,包括材料性质和边界条件。因此,数据的可靠性成为一个关键问题,尤其是在新材料的建模中。
3. 软件复杂性
有限元分析软件的复杂性可能对新手造成困扰,需要培训和经验来正确使用。因此,教育和培训变得尤为重要。
结论
有限元分析继续在工程领域发挥着关键作用,同时也面临着新的挑战和机遇。多物理耦合、拓扑优化和材料建模等新的前沿应用将继续推动这一领域的发展,为工程师提供更多工具来解决复杂的问题。然而,解决计算资源需求、数据可靠性和软件复杂性等挑战也将是持续的任务,以确保有限元分析能够持续发挥其作用。