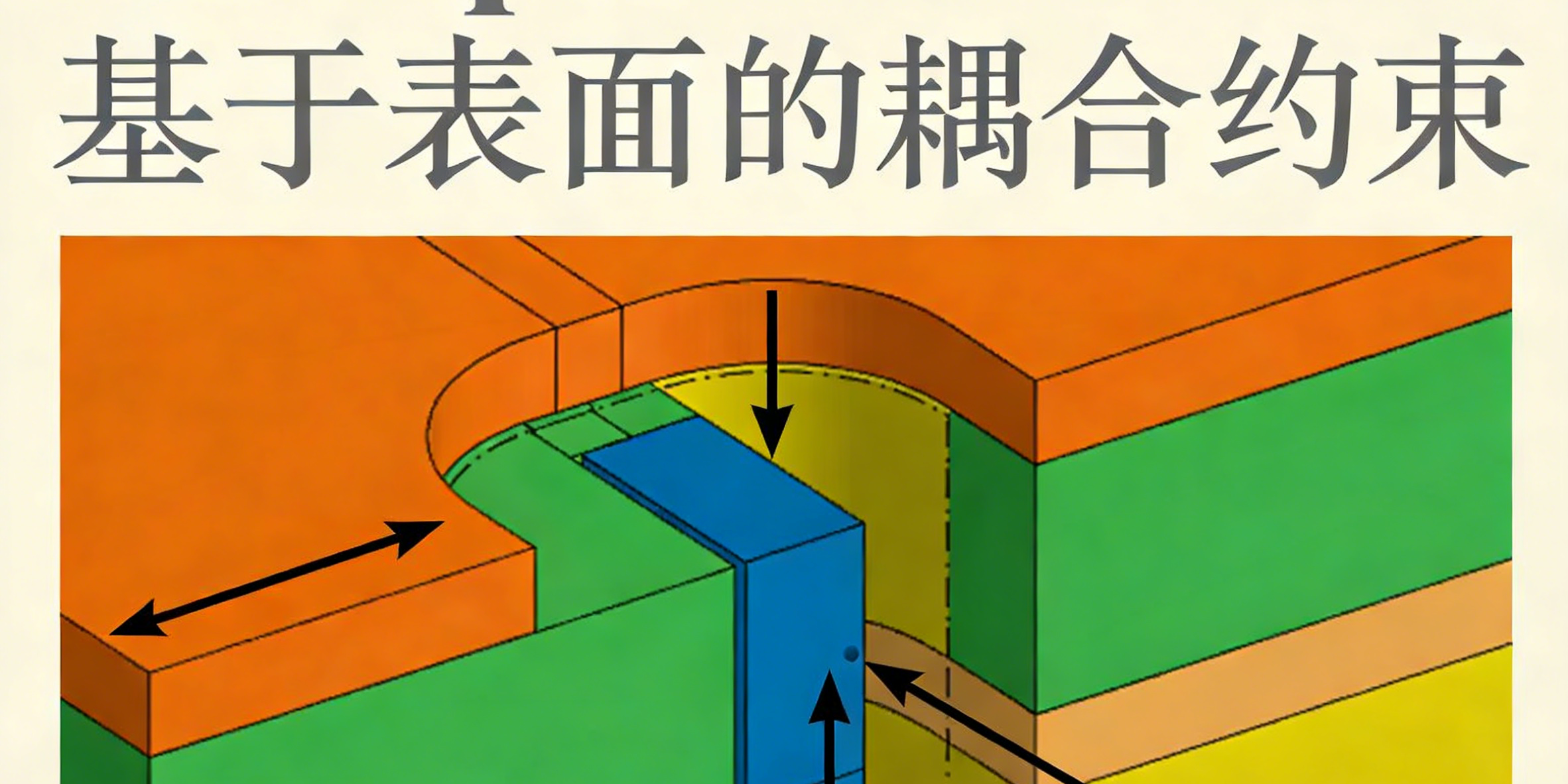
有限元分析已成为结构工程领域不可或缺的工具,使工程师能够模拟和分析各种条件下的复杂结构。在仿真软件提供的众多功能中,Abaqus因其先进特性而脱颖而出。本综合指南将深入探讨Abaqus的一项强大工具——基于表面的耦合约束。对于旨在进行准确高效结构仿真的工程师和研究人员而言,理解其细微差别和应用至关重要。
目录
I. 理解基于表面的耦合约束
II. Abaqus中基于表面的耦合约束的深入分析
III. 高级考量与最佳实践
IV. 局限性与最佳实践
V. 案例研究:球铰连接
VI. 结论
I. 理解基于表面的耦合约束
A. Abaqus 耦合约束简介
在 Abaqus 中,耦合约束对于建立表面节点与参考节点之间的连接至关重要。这种耦合主要通过两种类型实现:运动学耦合和分布耦合。
1. 运动学耦合
当需要将表面节点的运动约束为参考节点的刚体运动时,可采用运动学耦合。这确保了被约束的节点与参考节点保持刚性运动。
2. 分布耦合
分布耦合则通过为耦合节点指定权重因子来控制力的传递,从而提供更高的灵活性。此类耦合特别适用于需要约束平均运动而非刚体运动的场景。
B. 基于表面的耦合约束的应用
Abaqus 中的基于表面耦合约束具有广泛的应用场景,使其成为结构仿真中的多功能工具。一些典型应用包括:
1. 施加载荷与边界条件
基于表面的耦合约束可有效向模型施加载荷或边界条件。通过控制耦合节点的运动,可强制结构响应表现出特定行为。
示例:使用运动学耦合约束为模型预设扭转运动,同时不限制径向运动(见下图)。
2. 在模型上分布载荷
当载荷分布需遵循惯性矩表达式描述时,分布耦合约束提供了一种优雅的解决方案。经典的螺栓分布模式和焊缝分布模式等表达式非常适合此类应用。
示例:使用分布耦合约束在需要节点间相对运动的边界上规定位移和旋转条件。在此示例中,在结构末端施加了扭转约束,该末端预期会在端面内发生翘曲和/或变形(见下图)。
3. 维度过渡
基于表面的耦合在连续体单元与结构单元之间的过渡场景中具有重要价值。它能够实现模型中不同类型单元之间的灵活耦合。
4. 端部条件建模
运动学耦合定义可有效模拟端部条件,例如刚性端板或确保实体特定截面保持平面。
示例:使用运动学耦合模拟刚性端板,或保持实体截面为平面。
5. 简化复杂约束的建模
运动学耦合允许在局部坐标系中单独选择参与约束的自由度,从而简化复杂约束的建模过程。
6. 与其他约束的交互作用
耦合约束可与其他约束(如连接器单元)结合使用,以模拟真实的相互作用。
示例:使用运动学耦合与平移连接器模拟螺栓预紧力(若您希望深入探索该技术的细节,我们已撰写专题博客文章:《Abaqus 中的螺栓预紧技术》)。
C. 在 Abaqus 中定义基于表面的耦合约束
1. 定义耦合节点的步骤
定义耦合约束需指定参考节点、耦合节点及约束类型。耦合节点会根据指定的表面及可选的影响区域自动选择。
2. 运动学耦合约束
运动学耦合约束通过消除耦合节点的自由度来实现,确保其运动与参考节点刚性绑定。
3. 分布耦合约束
分布耦合约束通过引入权重因子来控制耦合节点处力和力矩的分布,从而灵活定义约束节点的行为。
II. Abaqus 中基于表面的耦合约束深度解析
A. 指定影响区域
默认情况下,耦合节点会为整个表面自动选择。但用户可通过定义影响半径,将耦合节点限制在以参考节点为中心的球形区域内。
1. 基于节点的表面
对于基于节点的表面,使用用户定义的权重因子。表面定义中指定的横截面积将作为权重因子。
2. 基于单元的表面的表面
对于基于单元的表面,权重因子由 Abaqus 自动计算。默认权重分布基于每个耦合节点的所属表面积(壳边缘表面则基于所属边缘长度)。该计算方式确保在指定影响半径时,默认权重分布能随半径平滑变化。
B. 分布约束的加权方法
分布耦合约束的默认权重分布基于所属表面积。用户可采用多种加权方法调整分布,灵活控制力传递。
1. 线性递减权重分布
可应用线性递减加权方案,即权重因子随与参考节点的径向距离线性减小。
让我们通过下图的模型来理解其工作原理。
若保持权重分布为均匀分布(默认选项),该部件将发生如下所示的变形。
若将权重分布设置为线性递减,该部件将发生如下所示的变形。
请注意,更多载荷被施加在中心节点上,并沿径向线性递减。
2. 二次多项式权重分布
二次多项式权重分布可基于径向距离实现更复杂的权重变化规律。
下图展示了同一部件采用二次多项式权重分布时的变形效果,即载荷沿径向呈二次函数规律递减。
3. 单调递减权重分布
单调递减权重分布采用三次多项式函数定义权重变化。
C. 指定局部坐标系
运动学耦合与分布耦合约束均可基于局部坐标系定义,从而更灵活地设定约束方向。
1. 基于局部坐标系的运动学耦合
运动学耦合可参照局部坐标系(而非全局坐标系)来定义约束关系。
2. 基于局部坐标系的分布耦合
类似地,分布耦合约束也可使用局部坐标系来定义约束方向。
3. 约束方向与有限旋转
在几何非线性分析步中,用于定义约束自由度的坐标系将随参考节点旋转。
III. 高级考量与最佳实践
A. 定义表面耦合方法
连续体耦合与结构耦合两种方法控制参考节点运动与耦合节点平均运动的关联方式。
1. 连续体耦合方法
默认的连续体耦合方法将参考节点的平动和旋转关联到耦合节点的平均平动,可分布力但不会传递力矩。
2. 结构耦合方法
结构耦合方法特别适用于壳单元的弯曲类应用,将参考节点的平动和旋转关联到耦合节点的平动与旋转运动。
B. 力矩释放与有限旋转
在几何非线性分析步中,定义力矩释放的自由度坐标系将随参考节点旋转。
C. 共线耦合节点排列
当耦合节点呈共线排列时,分布耦合约束可能无法传递力矩的某些分量,存在局限性。
IV. 局限性及最佳实践
尽管功能强大,Abaqus基于表面的耦合约束仍存在需要用户注意的局限性:
- 轴对称单元:无法用于发生非对称变形的轴对称单元
- 分布式耦合节点数量限制:过多耦合节点会导致内存占用显著增加且求解时间延长
为有效应对这些限制,需遵循以下最佳实践:
A. 优化耦合节点选择
谨慎选择耦合节点至关重要。对于包含大量节点的场景,策略性选择节点可显著提升计算效率。
B. 内存管理
针对耦合节点过多可能导致的高内存占用,用户应优化模型与仿真设置以有效管理计算资源。
C. 模型验证
在依赖仿真结果前,必须通过实验数据或已知解析解验证模型,确保仿真的准确性与可靠性。
D. 迭代优化方法
对于复杂仿真,建议采用迭代策略:先运行简化模型理解耦合约束行为,再将其应用于更精细的仿真中。
V. 案例研究:球铰连接
如图所示,某部件通过球头螺栓与另一部件连接。创建该连接器时,需为球头螺栓头部和球头螺栓座分别建立耦合约束,并通过连接器将这两个耦合的参考节点相连。
这种连接方式在车辆前后悬架系统中十分常见。例如:稳定杆与下拉杆之间、转向横拉杆与转向节之间、上控制臂与转向节之间的连接等。
您想了解更多关于球铰连接的信息吗?请点击此处查看相关博客文章。
下方视频将展示该模型的更多细节。
VI. 结论
总之,Abaqus中的基于表面耦合约束为工程师和研究人员提供了一个多功能且强大的工具,用于处理复杂的结构相互作用。无论是施加载荷、分布力、建模端部条件,还是促进与其他约束的交互,耦合约束都提供了全面的解决方案。了解其应用领域、有效定义约束以及应对其局限性,是充分发挥这一功能潜力的关键所在。
随着计算能力的持续进步,基于表面耦合约束在结构仿真中的应用预计将变得更加普遍。通过将这些技术纳入分析,工程师可以提高模型的准确性和效率,从而在结构工程领域为更安全、更具创新性的设计铺平道路。